alocaMatrizes

Este repositório contém um relatório e os programas usados para testes com alocação dinâmica de matrizes de uma única vez ou em varias etapas.

Project maintained by gradvohl Hosted on GitHub Pages — Theme by mattgraham

Teste de alocação de matrizes

Introdução

Esse relatório mostra alguns testes de alocação dinâmica de matrizes. A ideia é testar duas abordagens diferentes, no que se refere ao desempenho e à forma de utilização dessas estruturas de dados. Uma das abordagens é a alocação de matrizes em duas etapas: na primeira etapa ocorre a alocação das linhas (cada linha é um ponteiro para as colunas); e, na segunda etapa, a alocação de cada uma das colunas. A segunda abordagem é a alocação em uma única etapa, alocando toda a matriz em uma única dimensão, como se alocasse um vetor.

tl;dr É melhor utilizar a alocação em uma única etapa no seu código.

Motivação

A motivação para estes testes e também para este repositório veio de uma observação a respeito da forma como os estudantes alocavam as matrizes em trabalhos com múltiplos threads, na disciplina de Sistemas Operacionais. Como o tamanho das matrizes deveria ser especificado pelo usuário no início da execução do programa, os estudantes tinham que alocar essas matrizes dinamicamente.

Sendo assim, notei que a maioria deles usava a abordagem em duas etapas. Isso me incomodava muito, pois a abordagem em uma única etapa me parecia muito mais prática e mais rápida. Por esse motivo, resolvi fazer alguns testes e apresentar os resultados para demonstrar que a segunda abordagem é, de fato, mais eficiente. Além disso, ao registrar os métodos e resultados, espero esclarecer as dúvidas dos estudantes e ajudá-los a escrever um código mais rápido.

Abordagens

Conforme comentei na Introdução, há duas abordagens para alocação de matrizes em D dimensões. Vamos considerar D=2, por simplicidade, mas depois podemos generalizar. Consideraremos também que, para D=2, a matriz alocada terá n linhas (numLinhas) e m colunas (numColunas).

Alocação em D etapas

Uma das abordagens é a alocação de matrizes em D=2 etapas. Na primeira etapa será alocado espaço para n ponteiros, um para cada linha da matriz. Na segunda etapa, para cada um dos n ponteiros, será alocado um espaço para m valores.

Como exemplo, observe o código a seguir para alocar uma matriz de n x m números reais (float).

  // Declaração da matriz
  float **matriz;
  
  // 1ª etapa de alocação 
  matriz = (float **) malloc(numLinhas * sizeof(float *));
  
  // 2ª etapa de alocação
  for (i=0; i<numLinhas; i++)
      matriz[i] = (float *) malloc(numColunas * sizeof(float));

Note que, na declaração da matriz, esta é do tipo “float **” ou, em outras palavras, a matriz é um “um ponteiro para ponteiros para números reais”. Até aí, tudo bem em termos de ocupação de memória, pois um ponteiro ocupa poucos bytes.

Na 1ª etapa de alocação, utiliza-se o comando malloc para alocar os ponteiros. Note que, nos parâmetros para este primeiro comando malloc, estamos calculando o tamanho de um ponteiro para float e multiplicando pela quantidade de linhas. Note também que estamos fazendo uma conversão de tipos (cast) para o tipo float **.

A 2ª etapa inclui um laço em que, a cada iteração, chama-se o comando malloc para alocar um conjunto de números reais, na quantidade de colunas que desejamos que a matriz tenha.

Daí, já se pode observar que o processo de alocação de matrizes tem ordem M, ou seja, O(M). Em outras palavras, a criação de uma matriz com M colunas, vai gastar M iterações.

Entretanto, vejo que há um pequeno aspecto positivo nessa abordagem. O acesso aos elementos de uma matriz alocada dessa forma é feito da mesma forma que uma matriz convencional (alocada estaticamente). Em suma, você acessaria o elemento da linha i e coluna j da matriz utilizando matriz[i][j].

Contudo, esse aspecto positivo some um pouco na hora da especificação de uma função que recebe uma matriz de alocação dinâmica como parâmetro. Nesse caso, uma função que recebe como parâmetro uma matriz de números reais alocada dinamicamente deve ter a seguinte assinatura: funcao(float **matriz).

A generalização dessa abordagem para D dimensões é fácil de se obter. Basta adicionar mais laços, um para cada nova dimensão, e ajustar os limites e índices dos laços a cada nova dimensão a ser construída.

Alocação em uma única etapa

A alocação em uma única etapa inclui uma única chamada à função malloc, independente da quantidade de dimensões que a matriz terá. Essa razão já é, em teoria, suficiente para contraindicar a alocação em D etapas. Afinal, diferente da alocação em D etapas, nesse caso a ordem para alocação de uma matriz é O(1).

Para a alocação em uma única etapa, vamos utilizar a função malloc especificando o tamanho da matriz a partir da multiplicação da quantidade de linhas (numLinhas) pela quantidade de colunas (numColunas), multiplicado pelo tamanho do tipo de dados da matriz. Observe o código a seguir:

  // Declaração da matriz
  float *matriz;

  matriz = (float *) malloc(numLinhas * numColunas * sizeof(float));

Note que, na declaração da matriz, esta é do tipo “float *” ou, em outras palavras, a matriz é um “um ponteiro para números reais”. Isso porque, embora o malloc aloque espaço suficiente para todos os elementos da matriz, precisamos apenas do endereço da primeira posição. As demais serão calculadas a partir desse primeiro endereço.

Neste momento aparece um aspecto um pouco negativo dessa abordagem: a forma de acesso aos elementos da matriz. Aqui, é preciso lembrar que as matrizes na linguagem C – diferente da linguagem Fortran, por exemplo – alocam as matrizes estáticas no formato “linha primeiro”, ou seja, primeiro os elementos da primeira linha, depois os elementos da segunda linha, e assim por diante. Sendo assim, para acessar o elemento que está na linha i, coluna j, de uma matriz com numColunas, é preciso usar a seguinte fórmula matriz[i*numColunas + j].

Pode parecer estranho e deixar o código pouco legível, mas pode acreditar, funciona. E funciona um pouco melhor se as variáveis i, j e numColunas forem registradores, ao invés de variáveis alocadas na memória. O programador mais experiente na linugagem C pode inclusive criar uma definição (#define) para tornar o código mais legível. Por exemplo:

#define posicao(I, J, COLUNAS) ((I)*(COLUNAS) + (J))
...
   // Acesso à matriz
  valor = matriz[posicao(i, j, numColunas)];

A passagem dessa matriz como parâmetro para uma função é muito simples e, mais uma vez, não depende da quantidade de dimensões. Veja o exemplo a seguir: funcao(float *matriz).

A generalização dessa abordagem para D dimensões, supondo que as dimensões são o conjunto {d₁, d₂, … ,d_n} também é simples. Na alocação, basta multiplicar as dimensões entre si para calcular o tamanho da matriz. Para acessar a posição P, onde P é formado pelas coordenadas {p_d₁, p_d₂, … ,p_{d_n}}, basta calcular p_d₁ x d₂ + p_d₂ x d₃ + … + p_{d_n-1} x d_n + p_{d_n}.

Em um exemplo mais simples, suponha que você tem uma matriz com três dimensões (d₁ = linhas, d₂ = colunas, d₃ = profundidade) e você quer acessar a matriz nas coordenadas [i, j e k]. Então, o acesso será feito da seguinte forma matriz[i*colunas + j*profundidade + k].

Testes práticos

Se os argumentos sobre as Abordagens não foram suficientes para convencê-lo, mostro a seguir alguns testes que mostram que a abordagem em uma única etapa é, de fato, bem melhor. A metodologia e os programas utilizados para os teste são bem simples. Vamos à metodologia primeiro.

Metodologia

A metodologia utilizada foi a seguinte:

Criou-se duas versões de um mesmo programa, com uma única thread, cujo algorimo é descrito na seção sobre o Algoritmo. Cada versão utiliza uma abordagem diferente, mas o mesmo algoritmo básico.
Realizamos conjuntos de testes para matrizes de 10x10, 100x100 e 1000x1000 em cada abordagem, sempre medindo o tempo de execução em três trechos do programa: na alocação da matriz, na inserção de elementos na matriz e no acesso aos elementos da matriz.
Cada programa é executado 10 vezes e seus resultados coletados. É calculada uma média dos tempos das 10 execuções.
Comparamos os tempos médios de cada programa para cada tamanho de matriz.

Para deixar todo o processo o mais automatizado possível, foram criados scripts para automatizar os testes. Basicamente, o script vai rodar executar o programa indicado várias vezes e, entre uma vez e outra, espera um tempo aleatório (1, 2 ou 3 segundos) para tentar evitar otimizações do Sistema Operacional em relação à alocação de memória.

Algoritmo

O algoritmo que o programa vai executar é simples e se resume aos seguintes passos:

Aloca a matriz;
Insere elementos na matriz;
Lê os elementos da matriz.
Imprime os tempos de cada etapa de processamento.

Entre cada passo, calcula-se o tempo que aquela etapa consumiu. Para evitar a utilização de dispositivos de entrada e saída (E/S), no passo 2, os elementos inseridos na matriz são valores zero ou um, gerados aleatoriamente.

Resultados

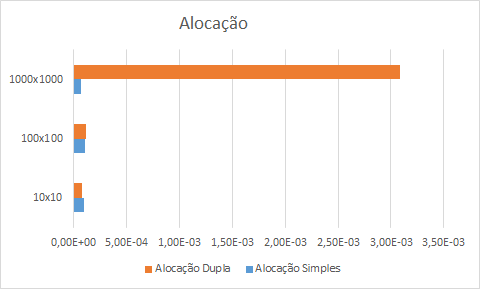
Os resultados são mostrados nas tabelas e gráficos a seguir. A primeira figura mostra o gráfico de alocação das matrizes, que é o trecho que mais consome tempo na primeira abordagem. Neste e nos demais gráficos, o eixo x mostra o tempo gasto (em segundos) em cada operação. No eixo y estão os tamanhos das matrizes (10 x 10, 100 x 100 e 1000 x 1000).

Alocação de Matriz .

Observe que, conforme discutimos previamente, na alocação em duas etapas, o tempo de alocação de uma matriz cresce quando o tamanho das dimensões cresce. Na alocação em uma única etapa, esse tempo sofre poucas variações. Algo interessante de notar é na alocação de matrizes pequenas (10 x 10). O tempo médio da alocação em duas etapas foi menor. No entanto, se considerarmos o desvio padrão os tempos se equivalem. A propósito, quando as matrizes têm grandes dimensões (1000 x 1000), a diferença é bastante significativa, da ordem de 45 vezes mais lenta.

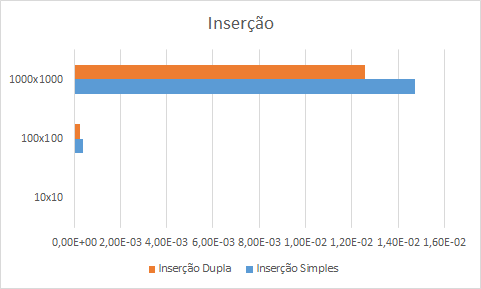
Vejamos o gráfico das operações de inserção. Aqui há outra surpresa que discutiremos na seção Discussões.

Inserção na Matriz .

Nesse caso, a inserção simples foi mais lenta em todas as dimensões de matrizes, cerca de 20% mais lenta. É pouco, mas é significativo.

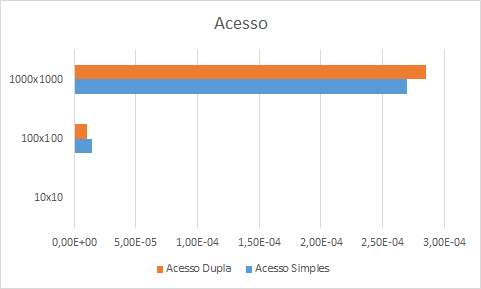
Finalmente, vejamos o gráfico das operações de acesso. Nesse caso, os tempos de acesso da alocação em duas etapas são maiores, quando as matrizes são maiores; mas são menores quando são matrizes são menores.

Acesso à Matriz .

As diferenças de tempo são tão sutis quanto no caso da inserção, com vantagens para a alocação em uma etapa.

Discussões

Nesta seção, discute-se os resultados dos testes. Como se observa nos gráficos, a alocação é um processo extremamente demorado e isso tende a ficar pior na alocação em D etapas, quanto maior for o número de dimensões.

Já as operações de inserção e acesso têm diferenças menores entre ambas as abordagens, como se esperava. Provavelmente, se compilarmos os códigos com otimizações essas diferenças diminuirão.

Conclusões e extensões desse trabalho

Ponderando todos os aspectos analisados, concluímos o seguinte:

A alocação em D etapas implica em um código maior (em números de linhas) e mais complexo no que se refere à quantidade de iterações para criar a matriz. No entanto, isso favorece um pouco mais a legibilidade do código.
A alocação em única etapa, por sua vez, deixa o código menos complexo e mais rápido no trecho em que a matriz é alocada. Entretanto, não há benefícios significativos na leitura ou armazenamento de dados na matriz.

Em suma, acredito que a alocação em uma única etapa é mais prática, mais rápida e no cômputo geral apresenta resultados melhores do que a alocação em D etapas.

Novos testes e extensões desse trabalho

Esse trabalho não calculou o tempo necessário para desalocar as matrizes (comando free). Entretanto, a sequência de passos é tão complexa quanto a alocação. O programador ainda deve se certificar que todas as dimensões foram de fato liberadas.

Portanto, uma possível extensão desse trabalho são os testes com o processo de desalocação da matriz. Além disso, é possível complementar esse trabalho com matrizes com mais dimensões ou de dimensões maiores.

Apêndice

Os códigos dos programas para teste, o arquivo makefile para compilação, o script para executar os testes, além dos dados gerados estão todos disponíveis nesse repositório. O procedimento para realização dos testes foi o seguinte:

Compilamos os programas utilizando o makefile.

Executamos o comando a seguir para gerar os arquivos de dados para o programa de alocação em uma única etapa.

for i in 10 100 1000 ; do ./exectestes.sh -p ./matrizesSimplesDinamicas.o -n $i -m $i -i 10 > teste${i}x${i}Simples.dat; done

De forma análoga, executamos o comando a seguir para gerar os arquivos de dados para o programa de alocação em uma duas etapas.

for i in 10 100 1000 ; do ./exectestes.sh -p ./matrizesDuploDinamicas.o -n $i -m $i -i 10 > teste${i}x${i}Duplo.dat; done

Assim, a partir dos dados coletados, geramos os gráficos.